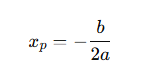Masuk SMA, banyak siswa mulai merasa matematika “naik level”.
Aljabar makin panjang, grafik mulai muncul, dan salah satu materi yang paling sering bikin bingung adalah fungsi kuadrat.
Padahal sebenarnya fungsi kuadrat itu tidak sesulit kelihatannya.
Kalau kamu paham bentuk dasarnya, hampir semua soal bisa diselesaikan tanpa menghafal banyak rumus.
Di artikel ini kita akan bahas dari nol sampai benar-benar paham.
Pengertian Fungsi Kuadrat
Fungsi kuadrat adalah fungsi yang memiliki pangkat tertinggi 2.
Bentuk umum:
y=ax2+bx+cy = ax^2 + bx + c
Keterangan:
-
a = koefisien x²
-
b = koefisien x
-
c = konstanta
Syarat:
a≠0a ≠ 0
Kalau a = 0 → bukan fungsi kuadrat (jadi fungsi linear).
Grafik Fungsi Kuadrat
Grafik fungsi kuadrat berbentuk parabola.
Ciri penting:
| Nilai a | Bentuk Parabola |
|---|---|
| a > 0 | terbuka ke atas |
| a < 0 | terbuka ke bawah |
Artinya:
-
a positif → punya nilai minimum
-
a negatif → punya nilai maksimum
Titik Puncak Parabola
Titik puncak adalah titik paling tinggi atau paling rendah pada grafik.
Rumus:
Setelah dapat x, masukkan ke persamaan untuk dapat y.
Contoh
y=x2−4x+3y = x^2 – 4x + 3
a = 1
b = -4
xp=−(−4)/(2×1)=2x_p = -(-4)/(2×1) = 2
Substitusi:
y=22−4(2)+3=−1y = 2^2 – 4(2) + 3 = -1
Titik puncak = (2 , -1)
Sumbu Simetri
Garis yang membelah parabola menjadi dua bagian sama.
x=−b2ax = -\frac{b}{2a}
Ternyata sama dengan rumus titik puncak!
Titik Potong Sumbu Y
Jika x = 0:
y=cy = c
Jadi titik potong sumbu Y = (0 , c)
Titik Potong Sumbu X
Gunakan pemfaktoran:
ax2+bx+c=0ax^2+bx+c=0
Contoh
x2−5x+6=0x^2 – 5x + 6 = 0
(x − 2)(x − 3) = 0
x = 2 atau x = 3
Diskriminan (D)
D=b2−4acD = b^2 – 4ac
Menentukan jumlah akar:
| D | Akar |
|---|---|
| D > 0 | dua akar |
| D = 0 | satu akar |
| D < 0 | tidak ada akar |
Contoh Soal Lengkap
Soal 1
Tentukan titik puncak:
y=x2−6x+5y = x^2 – 6x + 5 x=6/2=3x = 6/2 = 3 y=9−18+5=−4y = 9 – 18 + 5 = -4
Jawab: (3 , -4)
Soal 2
Tentukan akar:
x2−9=0x^2 – 9 = 0 (x−3)(x+3)=0(x-3)(x+3)=0
x = 3 atau −3
Soal 3
Tentukan jenis akar:
y=x2+4x+5y = x^2 + 4x + 5
D = 16 − 20 = −4
Tidak ada akar real
Latihan Soal
-
y = x² + 2x −3 → akar?
-
y = x² −8x +16 → titik puncak?
-
y = 2x² −4x → sumbu simetri?
-
y = x² −4x+4 → jenis akar?
-
y = −x² +6x−8 → maksimum?
Cara Cepat Memahami
Ingat konsep inti:
bagi dua b → titik tengah parabola
Tips:
-
tanda a menentukan arah
-
c titik potong Y
-
faktorkan untuk akar
Jadi tidak perlu hafal banyak.
Kesalahan Umum
-
Salah tanda negatif
-
Lupa bagi 2a
-
Tidak substitusi ke y
-
Bingung akar kembar
-
Salah hitung diskriminan
Penerapan Fungsi Kuadrat
Dipakai di:
-
fisika (gerak parabola)
-
ekonomi (keuntungan maksimum)
-
teknik (lintasan benda)
-
grafika komputer
-
AI dan simulasi
FAQ
Q: Kenapa grafik melengkung?
Karena ada pangkat dua.
Q: Apa arti titik puncak?
Nilai maksimum/minimum.
Q: Apakah selalu punya akar?
Tidak, tergantung diskriminan.
Q: Bagian terpenting?
Memahami bentuk parabola.
Q: Harus hafal semua rumus?
Tidak, cukup konsep.
Kesimpulan
Fungsi kuadrat bukan sekadar rumus, tapi pola bentuk.
Jika kamu tahu:
-
arah parabola
-
titik tengah
-
cara faktorisasi
maka hampir semua soal bisa dikerjakan dengan cepat.
Kuncinya bukan hafalan, tapi memahami bentuk grafik.

baca artikel sebelumnya:
Peluang (Probability): Pengertian, Rumus, Contoh Soal & Cara Cepat Menghitung Kemungkinan