Teorema Pythagoras dan Aplikasinya untuk Kelas 8 SMP

By
Fitria Ramadani
-
0
5

Matematika kelas 8 SMP mengenalkan salah satu konsep geometri yang sangat penting: Teorema Pythagoras. Materi ini berguna untuk menghitung sisi segitiga siku-siku dan sering muncul dalam soal cerita sehari-hari.

Dalam artikel ini, kita akan membahas secara lengkap:

  • Pengertian Pythagoras

  • Rumus dan cara cepat

  • Contoh soal dan cara penyelesaian

  • Latihan soal

  • Aplikasi dalam kehidupan sehari-hari

  • FAQ

1. Pengertian Teorema Pythagoras

Teorema Pythagoras menyatakan bahwa pada segitiga siku-siku, kuadrat panjang sisi miring (hipotenusa) sama dengan jumlah kuadrat panjang kedua sisi lainnya (sisi siku-siku).

Secara matematis:

c2=a2+b2c^2 = a^2 + b^2

Keterangan:

  • cc = panjang sisi miring (hipotenusa)

  • a,ba, b = panjang sisi siku-siku

Teorema ini ditemukan oleh Pythagoras, seorang matematikawan Yunani, dan menjadi dasar penting dalam geometri serta fisika.

1.1. Sifat Segitiga Siku-Siku

  • Salah satu sudut = 90°

  • Sisi yang berhadapan dengan sudut siku-siku = hipotenusa

  • Dua sisi lainnya = sisi tegak (siku-siku)

2. Rumus dan Cara Cepat Menghitung

2.1. Rumus Dasar

Jika diketahui dua sisi segitiga siku-siku:

  1. Diketahui kedua sisi siku-siku → cari hipotenusa:

c=a2+b2c = \sqrt{a^2 + b^2}

  1. Diketahui hipotenusa dan satu sisi → cari sisi lain:

a=c2−b2ataub=c2−a2a = \sqrt{c^2 – b^2} \quad \text{atau} \quad b = \sqrt{c^2 – a^2}

2.2. Cara Cepat

  • Kuadratkan panjang sisi yang diketahui

  • Jumlahkan (untuk hipotenusa) atau kurangkan (untuk sisi tegak)

  • Cari akar kuadrat hasilnya

3. Contoh Soal Pythagoras

3.1. Contoh 1: Mencari Hipotenusa

Segitiga siku-siku memiliki sisi 3 cm dan 4 cm. Tentukan panjang hipotenusanya.

Penyelesaian:

c2=a2+b2=32+42=9+16=25c^2 = a^2 + b^2 = 3^2 + 4^2 = 9 + 16 = 25 c=25=5c = \sqrt{25} = 5

Jawaban: Hipotenusa = 5 cm

3.2. Contoh 2: Mencari Sisi Tegak

Segitiga siku-siku memiliki hipotenusa 13 cm dan satu sisi 5 cm. Tentukan sisi yang lain.

Penyelesaian:

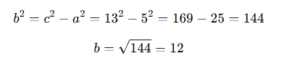
Jawaban: Sisi lainnya = 12 cm

3.3. Contoh 3: Soal Cerita

Seorang petani ingin membuat tangga dengan alas 6 m dan tinggi 8 m agar mencapai atap gudang. Panjang tangga (hipotenusa) = ?

Penyelesaian:

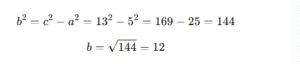
Jawaban: Panjang tangga = 10 m

4. Latihan Soal

Soal 1

Segitiga siku-siku memiliki sisi 7 cm dan 24 cm. Tentukan hipotenusanya!

Soal 2

Segitiga siku-siku memiliki hipotenusa 17 cm dan satu sisi 8 cm. Tentukan sisi yang lain!

Soal 3

Sebuah tangga tingginya 12 m, alasnya 5 m. Panjang tangga = ?

Soal 4

Segitiga siku-siku sama kaki memiliki sisi tegak 6 cm. Tentukan panjang hipotenusa!

Soal 5

Segitiga siku-siku memiliki hipotenusa 25 cm dan sisi tegak 15 cm. Tentukan sisi lainnya!

Kunci Jawaban:

  1. c = 25 cm

  2. sisi lain = 15 cm

  3. tangga = 13 m

  4. hipotenusa = √(6²+6²) = √72 ≈ 8,49 cm

  5. sisi lain = √(25² – 15²) = √400 = 20 cm

5. Aplikasi Teorema Pythagoras dalam Kehidupan Sehari-hari

  1. Membangun tangga → menghitung panjang tangga agar mencapai ketinggian tertentu

  2. Menentukan jarak titik → di peta atau koordinat

  3. Bangunan dan konstruksi → memastikan sudut siku-siku presisi

  4. Olahraga → misal lintasan diagonal lapangan

  5. Desain grafis & game → menghitung jarak antar titik di bidang

6. Tips dan Cara Cepat Mengingat

  1. Hipotenusa selalu dihadapkan pada sudut siku-siku

  2. Gunakan pola 3-4-5 atau kelipatannya untuk segitiga khusus (contoh: 6-8-10)

  3. Gunakan tabel kuadrat untuk menghitung cepat (misal 5² = 25, 12² = 144)

  4. Jika sisi tegak sama → segitiga sama kaki → hipotenusa = √(2 × sisi²)

7. FAQ Teorema Pythagoras

Q1: Apakah Pythagoras hanya berlaku untuk segitiga siku-siku?
A: Ya, teorema ini hanya berlaku pada segitiga dengan sudut 90°.

Q2: Bisa kah Pythagoras digunakan untuk menghitung jarak diagonal persegi?
A: Bisa, diagonal = √(sisi² + sisi²)

Q3: Bagaimana cara cepat menghitung segitiga dengan sisi kecil?
A: Gunakan pola 3-4-5, 5-12-13, atau kelipatannya.

Q4: Apakah kita bisa menggunakan Pythagoras di kehidupan nyata?
A: Ya, banyak aplikasi nyata: konstruksi, tangga, jarak, lapangan olahraga, desain.

Q5: Apakah bisa digunakan untuk segitiga tumpul atau lancip?
A: Tidak langsung. Untuk segitiga lain, gunakan hukum kosinus.

baca artikel sebelumnya:

Bangun Ruang dan Bangun Datar: Pengertian, Rumus, Contoh Soal, dan Latihan